Schwierigkeit 3
Schreiben Sie eine Java-main-Methode, in der die Werte von drei lokalen int-Variablen a, b und c aufsteigend sortiert werden. Verwenden Sie als Kontrollstruktur nur die if-Anweisung. Vertauschen Sie die Werte dieser Variablen so, dass zum Schluss a < b < c gilt. Prüfen Sie Ihre Methode mit allen Permutationen der Zahlen 1, 2 und 3 (es gibt insgesamt 6 Kombinationen). Nach der Ausführung Ihrer Anweisungen muss in all diesen Fällen also immer a=1, b=2 und b=3 gelten. Man kann die Aufgabe mit drei if-Anweisungen (ohne else) lösen, da im schlimmsten Fall drei Vertauschungen nötig sind.
Schwierigkeit 3
Schreiben Sie eine Java-main-Methode, in der das grosse Ein-Mal-Eins berechnet und tabellarisch auf dem Bildschirm ausgegeben wird. Um die auszugebenen Zahlwerte geeignet einzurücken, sollten Sie bei der Ausgabe den Tabulator "\n" verwenden. Verwenden Sie die for-Schleife.
Beim grossem Ein-Mal-Eins werden alle Produkte i * j mit 0 < i <= 10 und 0 < j <= 10 gebildet. Die Ausgabe sollte also etwa wie folgt aussehen:
1 2 3 4 5 6 7 8 9 10 2 4 6 8 10 12 14 16 18 20 3 6 9 12 15 18 21 24 27 30 4 8 12 16 20 24 28 32 36 40 5 10 15 20 25 30 35 40 45 50 6 12 18 24 30 36 42 48 54 60 7 14 21 28 35 42 49 56 63 70 8 16 24 32 40 48 56 64 72 80 9 18 27 36 45 54 63 72 81 90 10 20 30 40 50 60 70 80 90 100
Schwierigkeit 3
In der Klausur Informatik 1 können Sie maximal 120 Punkte erreichen. Bei 60 Punkte gilt die Klausur als bestanden (4,0). Für jede weiteren 5 Punkte verbessert sich die Note um eine Notenstufe. Für jeweils 5 Punkte weniger verschlechtert sich die Note um eine Notenstufe (bis 5,0). Aus rechtlichen Gründen gibt es keine 4,3 - sondern in diesem Fall auch eine 4,7. Es können auch halbe Punkte vergeben werden.
| Note | Punkte |
| 5,0 | 0 - 49,5 |
| 4,7 | 50 - 59,5 |
| 4,0 | 60 - 64,5 |
| 3,7 | 65 - 69,5 |
| 3,3 | 70 - 74,5 |
| 3,0 | 75 - 79,5 |
| 2,7 | 80 - 84,5 |
| 2,3 | 85 - 89,5 |
| 2,0 | 90 - 94,5 |
| 1,7 | 95 - 99,5 |
| 1,3 | 100 - 104,5 |
| 1,0 | 105 - 120 |
Implementieren Sie eine Java-Funktion, die für eine Punktzahl von 0 bis 120 die entsprechende Note berechnet und zurückgibt. Schreiben Sie eine Java-main-Methode, die für alle Punkte von 0 bis 120 in Schritten von 0,5 die zugehörige Note auf dem Bildschirm ausgibt.
Schwierigkeit 2
Implementieren Sie ein Java-Programm, das für einen Tag (1..31), den Monat (1..12) und das Jahr den zugehörigen Wochentag bestimmt und auf dem Bildschirm ausgibt.
Folgendes Verfahren berechnet diesen Wochentag für ein Datum, dass zwischen März 1900 und Februar 2100 liegt.
Zuerst muss die Gesamtanzahl der Wochentage von 1900 bis zum gegeben Datum errechnet werden (s.u.). Dies ist letztlich die Hauptschwierigkeit. Wenn diese Zahl berechnet ist, muss sie nur noch mit Rest durch 7 geteilt werden. Das ergibt den Wochentag, wobei 0 der Sonntag ist
Die Gesamtanzahl Wochentage berechnet sich schrittweise wie folgt:
Hier einige Daten mit Wochentagen zum Testen des Java-Programms:
(für Glückspilze)
Schwierigkeit 2
Eine "todsichere" Gewinnstrategie beim Roulettespiel ist es, immer auf die selbe Farbe zu setzen. Wenn man verloren hat, dann verdoppelt man einfach den Einsatz, um den vorherigen Verlust wieder wett zu machen. Die Wahrscheinlichkeit das immer rot (oder schwarz) kommt ist 50% (wir ignorieren das Auftreten der 0).
Implementieren sie eine Java-main-Methode, die berechnet, wieviel Geld man ungefähr als Kapital benötigt, wenn man 1 000 000 mal spielt und der Anfangseinsatz ein Euro ist.
Die Eintreffenswahrscheinlichkeit 50% kann man mit Math.random() < 0.5 überprüfen.
Wie viel Geld werden Sie mitbringen, damit Sie ihren Einsatz nicht verlieren?
Erweitern Sie ihr Java-Programm, so dass ausgehend von einem Startkapital berechnet wird, nach wie vielen Spielen sie mit dieser Strategie ihr Geld verloren haben.
Schwierigkeit 3
Eine Anzahl Bytes gegeben als int-Wert soll so mit Hilfe der metrischen Einheiten (K, M, G) auf dem Bildschirm ausgegeben werden, dass höchstens 3 Vorkommastellen angezeigt werden. Die Ausgabe soll in etwa wie folgt aussehen:
123 Byte sind 123.0 Byte 15323 Byte sind 15.323 KByte 15323000 Byte sind 15.323 MByte 1532300001 Byte sind 1.532300001 GByte
Verwenden Sie keine Schleifen (nur if-else). Die Ausgabeanweisungen dürfen ausschliesslich am Ende der main-Methode sein.
Schwierigkeit 2
Der englische Mathematiker John Wallis nutzte folgende Methode zur Berechnung der Zahl Pi:
Es heißt nach ihm benannt Wallissches Produkt. Programmieren Sie eine Java-Klasse WallisschesProdukt, welche eine Methode enthält, die das Wallissche Produkt bis zum n-ten Faktor berechnet und zurückgibt. Diese Klasse darf keine Ein-/Ausgabefunktionen wie System.out.println() enthalten. Schreiben Sie eine Testklasse WallisschesProduktTest, in der Sie in einer for-Schleife für alle n von 1 bis 1000 das Produkt ausgeben. Vergleichen Sie die berechneten Ergebnisse mit dem konstanten Wert Math.PI (etwa in dem Sie zusätzlich die Differenz ihres berechneten Wertes zu Math.PI ausgeben).
Schwierigkeit 2
Abundante Zahlen sind Zahlen deren Summe aller Teiler dieser Zahl außer der Zahl selbst größer ist als die Zahl. Ist die Summe gleich der Zahl, dann handelt es sich um eine vollkommene Zahl (auch perfekte oder ideale Zahlen genannt).
12 hat zum Beispiel die Teiler 1, 2, 3, 4 und 6. Deren Summe ist 16 > 12. Deswegen ist 12 eine abundante Zahl. 6 ist eine vollkommene Zahl, da 1 + 2 + 3 = 6 gilt.
Schreiben Sie ein Java-Programm, das für eine Zahl überprüft, ob Sie abundant bzw. vollkommen ist oder nicht. Finden Sie alle vollkommenen und ungeraden abundanten Zahlen von 1 bis 1000.
Schwierigkeit 3
Eine natürliche Zahl heißt Harshad-Zahl, wenn Sie durch ihre Quersumme teilbar ist.
777 ist durch 7 + 7 + 7 = 21 teilbar und damit eine Harshad-Zahl.
Schreiben Sie ein Java-Programm, das alle Harshad-Zahlen von 1 bis 100 berechnet und am Bildschirm ausgibt.
Schwierigkeit 1
Eine natürliche Zahl ist ein Palindrom, wenn die umgekehrte Reihenfolge ihrer Dezimalziffern identisch zur Zahl ist:
121 und 8813200023188 sind zum Beispiel Palindrome.
Die Zahl, die sich durch Umkehrung der Dezimalziffern eine Zahl n entsteht, kürzen wir ab als u(n).
Also gilt u(1236) = 6321.
Ausgehend von einer Zahl z kann man wie folgt versuchen, schrittweise ein Palindrom zu erzeugen:
p := z;
do {
p := p + u(z);
while ( p != u(p) );
Beispiel: Wenn wir mit z = 57 anfangen. Dann ist p = 57 + 75 = 132 nach dem ersten Durchlauf.
Nach dem zweiten Durchlauf gilt p = 132 + 231 = 353. Die Schleife bricht dann ab.
Wenn für eine Zahl z dieser Algorithmus nie terminiert, also endlos weiterläuft, dann
heißt z Lychrel-Zahl. Es ist derzeit nicht bekannt, ob es solche Zahlen überhaupt gibt!
Als kleinster Kandidat gilt 196.
Schreiben Sie ein Java-Programm, das derartige Palindrome im Intervall von 1 bis 1000 findet. Beachten Sie, dass Sie die Iteration nach eine vorgegebenen Obergrenze (< 2 000 000 000) abbrechen müssen, da sie sonst bei Lychrel-Zahlen nicht terminiert. Beachten Sie auch den gültigen Wertebereich von int bzw. long: die Zahlen werden immer grösser und es kann ein Überlauf auftreten.
Bei maximal 1 000 000 000 Iterationen habe ich folgende (bereits bekannte) Kandidaten für Lychrel-Zahlen gefunden: 196, 295, 394, 493, 592, 689, 691, 788, 790, 879, 887, 978, 986.
Alternativ gibt es zu diesem Algorithmus auch einen Wettbewerb, bei dem für alle n-stelligen Dezimalzahlen, die Zahl gefunden werden soll, bei dem am wenigsten Iterationen benötigt werden, um mit obigen Algorithmus ein Palindrom zu erzeugen. Diese Zahlen heißen verzögerte Palindromzahlen (delayed palindromic numbers). Rekordhalter für 19-stellige Dezimalzahlen ist derzeit 1 186 060 307 891 929 990.
Schwierigkeit 2
Zwei Primzahlen p und q heissen Primzahlzwilling (oder Primzahlpaar), wenn ihre Differenz 2 ist. 3 / 5, 5 / 7, 11 / 13 sind zum Beispiel die ersten drei Primzahlzwillinge.
Implementieren Sie ein Java-Programm, welches alle Primzahlzwillinge bis zu einer vorgegebenen Obergrenze berechnet und auf dem Bildschirm ausgibt. Verwenden Sie zur Berechnung aller Primzahlen von 2 bis zur Obergrenze dieses Primzahlsieb
Schwierigkeit 2
Logische Rätsel lassen sich formal oft auflösen, indem man Sie aussagenlogisch formuliert.
Im folgenden Rätsel von Raymond Smullyan geht es um einen Hutmacher, einen Schnapphase und eine (Hasel-)Maus. Unter diesen drei Verdächtigen gibt es einen Dieb. Die Ermittlungen haben folgendes ergeben:
hutmacher,
schnapphase und maus codiert werden. Diese sollen genau dann
true sein , wenn die entsprechende Person der Dieb ist.
Wir verwenden die Java-Operatoren !, &, ^, | (und => als Implikation). Die aus den Ermittlungen formalisierten Erkenntnisse sind:
A => B kann durch ! A | B ersetzt werden.
Implementieren Sie ein Java-Programm, mit dem derartig formalisierte Rätsel gelöst werden können. Das Rätsel ist gelöst, wenn man eine Belegung der booleschen Variablen gefunden hat, so dass jede der Formeln war ist. Dazu kann man einfach alle Kombinationen der Belegungen aufzählen und ausprobieren. Für die drei booleschen Variablen gibt es 23 mögliche Kombinationen. Das Programm berechnet also die Wahrheitstafel für die Formel.
Alle Kombinationen für n boolesche Variablen können Sie über fortgesetztes Inkrementieren einer int-Zahl z bekommen: die Folge der 0en und 1en in der Binärcodierung der Zahl gibt ihnen die booleschen Wahrheitswerte für die zugehörige boolesche Variable an.
Wenn das dritte Bit von z den Wahrheitswert für die boolesche Variable schnapphase
angeben soll, dann bekommen Sie zum Beispiel den booleschen Wert mit
schnapphase = (z / 4 % 2) == 1
Schwierigkeit 3
Die Zahl Pi kann wie folgt näherungsweise im kartesischen Koordiantensystem über die Kreisgleichung x2 + y2 <= r bestimmt werden.
Wir nehmen r = 1. Es werden n zufällige Koordinate (x,y) im Bereich (0,0) und (1,1) erzeugt. Über die Kreisgleichung kann bestimmt werden, wie viele davon sich im Einheitskreis befinden. Die Anzahl Punkte im Einheitskreis oder im Quadrat ist proportional zur Fläche. Das Vierfache des Verhältnis Flache Quadrat zu Fläche Einheitskreis nähert sich deswegen Pi an. Siehe dazu folgende Abbildung:
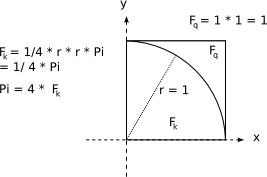
Programmieren Sie ein Java-Programm, das für ein n die Zahl Pi mit dieser Methode näherungsweise berechnet und auf dem Bildschirm ausgibt. Sie können Zufallszahlen zwischen 0 und 1 mit Math.random() erzeugen.
Schwierigkeit 3
Schreiben Sie ein Java-Programm, das zu einer ganzen Zahl alle Teiler auf dem Bildschirm ausgibt.
Schwierigkeit 3
Wir betrachten eine fiktive Hausratversicherung, bei der die Prämie wie folgt von der Anzahl Personen personen und
Quadratmeteranzahl flaeche der Wohnung abhängt:
| personen | Prämie |
| 1-2 | 10 + flaeche / 2 |
| 3 | 15 + flaeche |
| 4 | 15 + 1,5 * flaeche |
| >4 | 25 + 2 * flaeche |
Welche Kontrollanweisung eignet sich für die Implementierung am besten?
Schwierigkeit 2
Gegeben sei eine Folge von ganzen positiver Zahlen. Die Anzahl der Zahlen ist im Voraus nicht bekannt. Diese Zahlen werden vom Benutzer online über die Konsole eingegeben.
Gesucht ist das Minimum der Zahlen. Das Programm wird durch Eingabe einer negativen Zahl beendet. Es soll dann das gefundene Minimum auf dem Bildschirm ausgeben.
Algorithmen zu Problemen, bei denen die Eingabemenge vorab nicht bekannt ist, werden online-Algorithmen genannt.
Implementieren Sie eine main-Methode, die dieses Problem löst. Zur Eingabe von Zahlen können Sie die Klasse Eingabe.java verwenden. Sie enthält eine statische Methode readInt(), die eine neue Zahl von der Tastatur einließt und als int-Wert zurückgibt.
Schwierigkeit 3
Wir betrachten folgende unendliche Reihe, welche die Summe der Kehrwerte aller 2er-Potenzen berechnet.
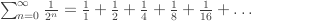
Diese Reihe konvergiert gegen einen konstanten Wert.
Implementieren Sie ein Java-Programm, welche diesen Grenzwert bestimmt. Implementieren Sie dazu eine Schleife, die solange die nächste 2er-Potenz zum bisherigen Teilergebnis hinzuaddiert, bis sich das Resultat nicht mehr ändert. Dies stell den - vermutlichen - Grenzwert der Reihe dar.
Schwierigkeit 2
Im Jahr 1742 hat Christian Goldbach eine Vermutung aufgestellt, nach der jede ungerade Zahl größer als fünf als Summe dreier Primzahlen dargestellt werden kann.
Die nach ihm benannte Goldbachsche Vermutung lautet in einer stärkeren, heute gebräuchlichen Version:
Jede gerade natürliche Zahl (größer als zwei) kann als Summe zweier Primzahlen repräsentiert werden.
Beispiele sind: 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, …
Die Summe muß nicht eindeutig sein: 5 + 5 = 3 + 7 = 10 .
Die Vermutung wurde bisher nicht bewiesen. Sie wurde für alle Zahlen bis 1018 (Stand 2007) bestätigt.
Implementieren Sie ein Programm, daß für alle geraden Zahlen bis zu einer Obergrenze, zwei Primzahlen findet, deren Summe gleich der Zahl ist. Verwenden Sie das Primzahlsieb zur Berechnung aller Primzahlen bis zu dieser Obergrenze (die Klasse Primzahlsieb.java ist in den Lösungen zu den Aufgaben enthalten).
Schwierigkeit 2
Eine natürliche Zahl n ist eine Giuga-Zahl, wenn alle ihre Primteiler p den Wert n/p - 1 teilen.
Implementieren Sie Java-Programm, die alle Giuga-Zahlen bis zu einer festen Obergrenze ausgibt.
Hinweis: Jede Primzahl ist eine Giuga-Zahl. Es ist derzeit (2008) nicht bekannt, ob die Umkehrung dieser Aussage gilt. Ihr Programm müsste also alle Primzahlen als Giuga-Zahlen identifizieren (und sonst keine).